對運輸汽車的衡稱重采樣點確定過程的優化,能夠有效提高汽車的衡稱重的精度。對地磅稱重采樣點的確定,需要 篩除衡稱重過程的粗大誤差,利用平方根矩陣對稱重采樣點進行優化,完成衡稱重精度的優化。傳統方法先推導出稱重測 量系統傳遞函數關系,并進行了離散化處理,但忽略了對稱重采樣點進行優化,導致精度優化效果不理想。提出基于采樣點 自適應確定優化的運輸地磅稱重方法,首先計算運輸地磅稱重時的位置誤差,并利用最小二乘法進行擬合求解;然后計 算運輸汽車的定位誤差相似度和標準差,去除冗余信號;最后利用3»準則篩除運輸地磅稱重的粗大誤差并進行求和,取 平均值作為經過稱臺的運輸汽車軸重測量值;在此基礎上,利用平方根矩陣對運輸地磅稱重的基礎采樣點進行優化。仿 真結果證明,所提方法能夠提高運輸地磅稱重的精度,對車輛運輸的現代化管理具有重要意義。
1.引言
隨著我國經濟的持續增長,道路工程和物流運輸業等得 到了推動性發展性,然而伴隨著交通事故的頻發,其中車 輛超速、超載行駛問題成為事故發生的主要因素。由于車 輛超載等一系列問題的產生,對人們生命財產安全和道路等 公共設施構成了極大威脅H。運輸汽車衡稱重管理系統是 測量車輛輪胎受力并計算其重量的過程H。為了促進車輛 運輸的現代化管理,降低車輛的超載對路面造成的破壞,需 要對運輸汽車衡稱重方法進行研究。傳統的基于過采樣技術的運輸汽車衡稱重方法,首先對車輛的運動狀態以及 動力特性進行分析;然后對運輸地磅稱重采樣數據進行采 集,利用過采樣技術處理采集到的汽衡稱重數據;最后利用 硬件電路系統實現對車輛的稱量。存在測量誤差率較大的 問題,為了獲得高精度的運輸汽車衡稱重值,成為了相關人 士的重點研究課題,為此提出了許多較為有效的方法。
文獻通過分析運輸地磅稱重力學模型,推導出運 輸地磅稱重測量系統傳遞函數關系,并進行了離散化處 理;然后利用最小二乘法估計運輸地磅稱重測量系統的模 型參數,進而推算出運輸汽車的實際重量。該方法存在運輸地磅稱重測量精度較低的問題。文獻主要利用運輸汽 車衡稱重徑向基函數神經網絡逼近運輸地磅稱重多路傳感器之間的函數關系,預測各個傳感器的數據輸出;然后將 各個傳感器的運輸汽車衡稱重預測信號和實際測量信息輸 入,建立信息融合運輸汽車衡稱重檢測模型,實現運輸汽車 衡稱重傳感器故障診斷;最后依據診斷結果獲得運輸汽車實 際重量。該方法由于運用了多路傳感器,存在測量誤差較 大、測量可靠性較低的問題。文獻的運輸地磅稱重方法,主要利用運輸汽車軸重稱量,即分別測量出運輸汽車各 個軸的軸重,再由測試系統計算出整個運輸汽車的實際重 量。該方法由于存在許多外界干擾,容易造成測量精度較低 的問題。
針對前面闡述方法出現的一系列問題,提出一種基于采 樣點自適應確定優化的運輸地磅稱重方法,通過仿真驗 證,所提方法能夠獲得高精度的測量結果,具有重要的現實 意義。
2.運輸地磅稱重量精度優化原理
在對運輸汽車進行稱重時,首先計算運輸汽車和稱臺的 振動方程,推導出汽運輸汽車和稱臺的傳遞函數并進行離散 化處理;然后利用最小二乘法估計運輸汽車和稱臺的模型參 數,進而推算出運輸汽車的實際重量。
假設M表示運輸汽車的質量,包括運輸汽車車身的質 量Ma和運輸汽車車轎的質量Mb (運輸汽車輪胎質量故略不 計);K表示運輸汽車和稱臺的剛度;C表示運輸汽車和稱臺 的阻尼系數。則運輸汽車和稱臺的振動方程表現為
MX + CX + KX = F (1)
式中,Z表示運輸汽車和稱臺的振動移位,包括運輸汽車車 身的振動移位又(t),運輸汽車車轎的振動移位Xt (t),運輸 汽車稱重稱臺的振動移位Xit)。
假設上述式(1)中的運輸汽車和稱臺的阻尼系數C為 零,得到兩個獨立的運輸汽車和稱臺振動方程,將上述式(1) 進行Laplace變換,則運輸汽車和稱臺輸出位移量X(t)和運 輸汽車和稱臺動態輸入載荷F(t)之間的傳遞函數計算表達 式如下
X( t)
G( t)
F( t)
輸入運輸汽車和稱臺信號U(t)的波形在理想狀態下是 個等腰梯形,則U(t)的計算公式為
u(t)=丄[r(t) - r{t - £o)-
to — £"o) + T (t — to — 2so)]
其中,r代表運輸汽車和稱臺采樣間隔;^o代表運輸汽車車 輪進入和離開稱重稱臺所用的時間;to代表運輸汽車在稱重 稱臺上行駛的時間;nt - to)代表時延為t的運輸汽車單位 速度信號。在運輸汽車衡稱重實際測量過程中獲得的是離 散信號,則上述式(3)對應的運輸汽車和稱臺的離散傳遞函 數具有以下形式:
 bo + 厶1 z + b2 z + 63 z 3 + 64 z 4 + 65z 5 + b6z 6
bo + 厶1 z + b2 z + 63 z 3 + 64 z 4 + 65z 5 + b6z 6
式中,表示運輸汽車和稱臺的Z變換系數;^1、、、 «6、bo、b、h、b3、b4、b5、b6表示運輸汽車和稱臺的參數,由測 量結果識別獲得。則運輸汽車和稱臺的差分方程為
«1 g(n - 1) + a2g(n -2) + 03g(n -2) + 04g(n -2)
+ 05g (n - 2) + a6g (n 一 2) = 6。x: (n) + 6。
x: (n) +
厶1 x (n) + 62 x (n) + 63 x (n) + 64 x (n) + 65 x (n)
+ 66x (n) (5)
其中,(n)表示運輸汽車和稱臺的階躍輸入,即離散化的運 輸汽車重量序列;當n名6時
g(n -2) = g(n - 3) = g(n -4)
=g(n -5) = g(n -6) = g(n) (6)
由于運輸汽車垂向位移x; (n)與運輸汽車和稱臺的傳感 器信號輸出v(n)成正比,則
g (n) = 6'ov (n) + 6'1 v (n - 1) + 6'2v (n - 2) + 6'3v (n -3)
+ 6'4v (n-4) + 6'5v (n-5) + 6'6v (n-6) + w (n) (7)
式中,《(n)表示運輸汽車稱重環節引入的誤差,6\v表示噪 聲利用最小二乘法估計模型參數。利用上式(7)即可實現抑 制測量噪聲的目的。
利用最小二乘法估計上式(7)中的參數6';v,計算g (n) 取平均值獲得運輸汽車的實際重量。
綜上所述為運輸汽車衡稱重的采樣點姿勢運營確定方 法原理,根據此原理完成對汽車衡稱重精度的優化。
3.運輸地磅稱重量精度優化方法
3.1基于采樣點自適應確定的信號采集和分析
首先計算運輸地磅稱重信號和運輸汽車運動學方程; 然后計算運輸汽車的位置誤差,并利用最小二乘法進行擬合 求解;最后利用空間差值原理,計算運輸汽車的定位誤差相 似度。具體步驟描述如下
假設m(t')表示運輸汽車軸重的真實信號;n' (t')表示 伴隨運輸汽車軸重真實信號m(t')的噪聲;則運輸地磅稱 重信號y (t')表示為
y( t') =m (t ) + n (t ) (8)
其中,運輸汽車軸重真實信號m(t')可以表示為 {M'汽車輪胎壓上稱臺 {o 其余
式中,M'表示運輸汽車某個軸的軸重真實值。
假設人表示運輸汽車相鄰兩個軸之間的空間變換關 系,利用采樣點自適應確定方法建立的J自由度運輸汽車運 動學方程表示為
7J = A1A2 …冷 (1o)
其中
= rot (z',) trans (z', ) trans (x, a;) rot (x, a;) rot (y,,;) (11)
式中,化表示運輸汽車運動學參數。運輸汽車的 位置誤差可以用運輸汽車運動學參數誤差的線性組合形式 表示Ap = J1 AOi + J2 Adt + J3 Aat + J4 Aa; + J5 (12) 式中,A(9;、Adi、Aa;、Aa;、AS;表示第i個軸的運輸汽車運動 學參數誤差。
將上式化簡可得
Ap = J- Ap (13)
其中,Ap表示運輸汽車的運動學參數誤差向量。采用最小 二乘法進行擬合求解可得
Ap = (JTJ) 1JT Ap (14)
根據上式計算獲得的運輸汽車運動學參數誤差可以估 計運輸汽車上稱臺的定位誤差。
則運輸汽車的定位誤差相似度計算表達式為
1 N( h)
r(h) = 2^g [ Ap(e{i')) - Ap(e{i') +h) ]2 (15)
式中,e'~ i')代表運輸汽車衡稱重時第r個采樣點的軸輸入;Ap (e{ i))代表該采樣點對應的運輸汽車衡稱重實際測量定位誤 差;h代表運輸汽車軸空間中兩個軸輸入的分割量,即軸輸 入在軸空間中的歐氏距離;(e{i) + h)代表與的分割量為 h的軸輸入;N(h)代表滿足分割量為h的點對的個數。
利用空間差值原理,運輸汽車目標點pl0)的定位誤差估 計值可以用已知采樣點的定位誤差線性組合表示,其表達式 如下
a p^ =乏一')Af (16) i = 1
式中,A^,(0)表示運輸汽車目標點pl0)在*軸上的定位誤差 估計值,在y軸和z上的定位誤差估計值計算同理;w'f'表示 運輸汽車目標點Pw在*軸上的權重;Ap':i')表示采樣點pi') 在:軸上的的定位誤差真實測量值;在y軸和z軸上的相關 參數計算同理。
3.2基于采樣點自適應確定的信號處理
依據3. 1節對運輸汽車的定位誤差相似度計算結果,首 先計算運輸地磅稱重標準差,去除運輸汽車經過稱臺時的 冗余信號;再利用3£準則篩除運輸汽車衡稱重的粗大誤差, 并對篩除粗大誤差后的信號進行求和,取平均值作為經過稱 臺的運輸汽車軸重測量值。詳細操作過程如下:
假設對被測量運輸汽車進行等精度測量,獲得獨立的測 量值&,2,其算術平均根為
,珋=士 X:i (17)
n i = 1
則運輸汽車定位剩余誤差為
vi = :i -X (18)
按照貝塞爾公式計算運輸汽車衡稱重標準差,其表達為
e = lin /— g (:i -x)2 (19) 一槡 n
假設運輸汽車衡稱重的某個測量值表示為的剩余誤 差vt (1 ^b^n),且滿足以下條件
I = \xb -X I > 3 (20)
則判斷Xb是包含粗大誤差的壞值,應該篩除,將篩除后的運 一 78 — 輸地磅稱重剩余數據繼續采用3e準則,直到將所有獲得 的壞值篩除為止。
根據上述式(20),將運輸地磅稱重數據篩除粗大誤差 后的數據進行求和,取平均值作為經過稱臺的運輸汽車軸重 測量值,完成基于采樣點自適應確定的運輸汽車衡稱重。
3.3運輸地磅稱重采樣點自適應確定方法優化
根據運輸地磅稱重精度補償的應用需求,在3. 1節運 輸汽車衡稱重信號采集的基礎上,分析運輸汽車衡稱重最優 采樣點具備的特征;然后計算運輸汽車衡稱重的最優采樣點 數學模型;最后利用平方根矩陣對運輸汽車衡稱重的基礎采 樣點進行線性變換得到濾波采樣點,實現采樣點自適應確定 方法的優化,具體過程描述如下:
分析運輸汽車衡稱重最優采樣點具備的特征:
1)采樣點個數最少;
2)最優采樣點能夠使得運輸汽車所有目標點在精度補 償后的剩余誤差之和最小;
3)最優采樣點需要在指定的工作范圍內選擇;
4)最優采樣點需要使得運輸汽車衡稱重時的各個目標 點在精度補償后的剩余誤差在給定的精度要求區間內。
根據上述分析,運輸汽車衡稱重的最優采樣點數學模型 計算公式如下
min/1 = Q (21)
L
minf2 = g I Ap, - Ap^ 1 (22)
i'=1
「1 在 e(i')在 ru
s. t. { u (23)
11 a, - ApUi') 1 在 s
式中,<?表示運輸地磅稱重最優采樣點集合包含的元素數 目;L表示運輸地磅稱重目標點(待精度補償點)的數目; Ap:']表示運輸地磅稱重目標點在精度補償前的原始定位 誤差;運輸汽車衡稱重目標點在精度補償后的剩余誤差大小 表示為| ApM - ApU:') ;r1和r“分別表示運輸汽車各個軸角 的上下限約束,是運輸汽車衡稱重的空間范圍;s表示運輸地磅稱重實際工程應用中的定位精度要求。
根據上述計算,利用平方根矩陣對運輸汽車衡稱重的基 礎采樣點進行線性變換得到濾波采樣點,其表達式為
^i = DkUk 槡A7槡7槡^qt (24)
其中,槡7表示運輸汽車衡稱重協方差矩陣qk的平方 根矩陣。
將上述式(23)和(24)相結合,即可實現運輸汽車衡稱 重采樣點自適應確定方法的優化。
4.仿真結果與分析
仿真的實現采用Visual C++和Matlab7. 0混合編程,實 驗將傳感器與信號測量系統進行并聯,對運輸汽車衡稱重稱 臺的實際采集信號進行處理,其中信號采集利用單片機,信號采集頻率為300Hz。實驗數據來源于某運輸地磅稱重 系統稱臺采集到的5000個信號,隨機選取其中2500個進行 仿真。
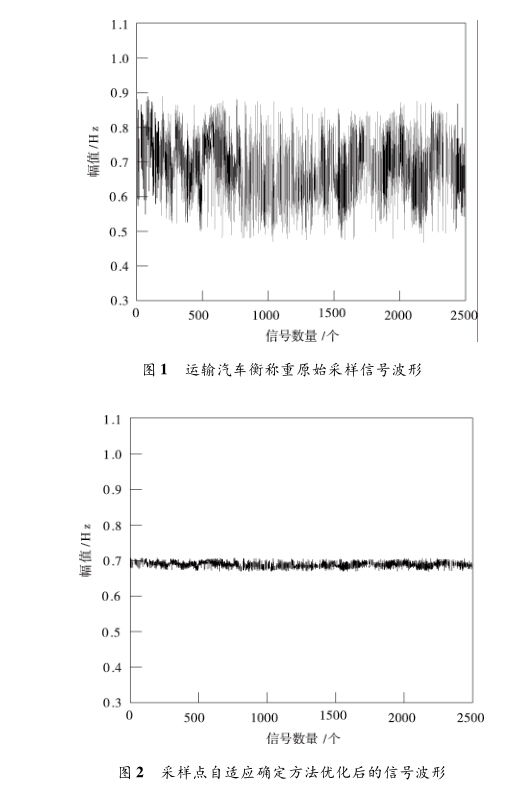
利用采樣點自適應確定方法采集的運輸汽車衡稱重信 號含有多種噪聲成分,其波形如圖1所示。
根據圖1可以看出,利用采樣點自適應確定方法采集的 運輸汽車衡稱重信號由于包含了較多的噪聲成分,使得采集 到的信號幅值最高為0. 9左右,最低在0. 5,誤差較大,容易 造成運輸汽車定位精度不高,從而導致實際稱重誤差較大的 問題。
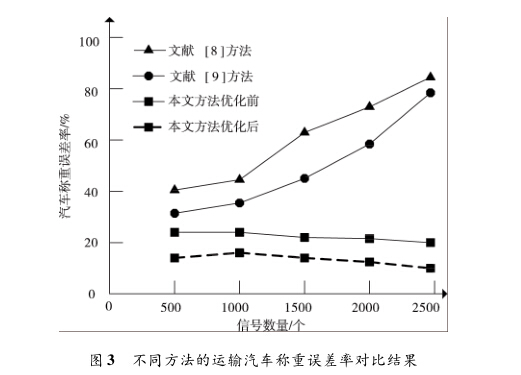
從圖2中可以看出,利用平方根矩陣對運輸汽車衡稱重 的基礎采樣點進行線性變換得到濾波采樣點信號很好地抑 制了噪聲影響,將采集到的信號幅值均控制在0. 7的范圍 內,大大改善了信噪比,為后續提高運輸汽車稱重精度提供 了良好的數據基礎。
為了進一步驗證所提方法有效性,采用文獻、文獻 方法與所提方法優化前后的運輸汽車稱重誤差率(% ) 進行對比分析,對比分析結果如圖3所示。
定義運輸汽車稱重的誤差率計算公式
戶生古地磅稱重測量值-汽車實際重量..inn~ 誤差率= 汽車實際重量 x
從圖3中可以看出,文獻H方法的運輸汽車稱重誤差率最 大;文獻9]方法的運輸汽車稱重誤差率次之;所提方法采用 的采樣點自適應確定方法的運輸汽車稱重平均誤差率為 20%左右,且誤差率相對平穩;采樣點自適應確定方法優化 后,將運輸汽車稱重誤差率降低到了 10%以內,在運輸地磅稱重管理系統,這樣的誤差率幾乎可以忽略不計,說明了 所提方法優化后的有效性。
5.結束語
采用當前方法對運輸汽車進行稱重時,測量誤差較大, 為此提出一種基于采樣點自適應確定優化的運輸地磅稱 重方法,仿真結果結果驗證了該采樣點優化方法的有效性, 對減小稱重誤差率具有良好的實用價值。



